Bayesian/Frequentist Tutorial

[1]:

import arviz as az
import bambi as bmb
import numpy as np
import pandas as pd
import pymc3 as pm

import matplotlib.pyplot as plt

from pymer4.simulate import simulate_lm, simulate_lmm
from pymer4.models import Lmer, Lm
from scipy.stats import ttest_ind

/home/osvaldo/anaconda3/lib/python3.7/site-packages/rpy2/robjects/pandas2ri.py:14: FutureWarning: pandas.core.index is deprecated and will be removed in a future version.  The public classes are available in the top-level namespace.
  from pandas.core.index import Index as PandasIndex
INFO:numexpr.utils:NumExpr defaulting to 4 threads.

[2]:

az.style.use('arviz-darkgrid')
In this notebook we demo how to perform the same set of analyses using a frequentist approach and a bayesian approach.
We’ll perform two sets of analyses:
1) Simple between groups t-test (i.e. univariate regression with dummy-coding)
2) Multi-level multivariate regression model (with two predictors)
We’ll estimate the frequentist statistics using pymer4.

Generate t-test data

[3]:

a = np.random.normal(5,2,1000)
b = np.random.normal(8,2.5,1000)
df = pd.DataFrame({'Group':['a']*1000 + ['b']*1000,'Val':np.hstack([a,b])})

[4]:

df.groupby('Group').describe()

[4]:
Val
count mean std min 25% 50% 75% max
Group
a 1000.0 4.901747 1.955774 -0.900373 3.586848 4.961405 6.163554 11.872290
b 1000.0 7.975125 2.518749 -2.232115 6.278875 8.002316 9.669793 14.847826 
[5]:

f,ax = plt.subplots(1,1,figsize=(8,6))
ax.hist(a,alpha=.5,bins=50);
ax.hist(b,alpha=.5,bins=50);
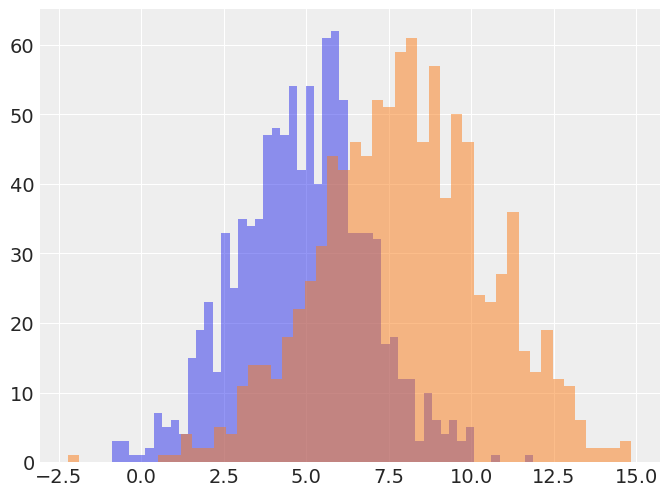
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_7_0.png

Frequentist

Since this analysis is relateively straightforward we can perform a between groups t-test using scipy

[6]:

ttest_ind(b,a)

[6]:

Ttest_indResult(statistic=30.477105041971846, pvalue=7.2541984106044045e-168)

We can also set this up as a dummy-coded univariate regression model which is identical

[7]:

# Using the pymer4 package, but we could have used statsmodels instead
model = Lm('Val ~ Group',data=df)
model.fit()

Formula: Val~Group

Family: gaussian         Estimator: OLS

Std-errors: non-robust  CIs: standard 95%       Inference: parametric

Number of observations: 2000     R^2: 0.317      R^2_adj: 0.317

Log-likelihood: -4463.088        AIC: 8930.176   BIC: 8941.378

Fixed effects:


[7]:
Estimate 2.5_ci 97.5_ci SE DF T-stat P-val Sig
Intercept 4.902 4.762 5.042 0.071 1998 68.742 0.0 ***
Group[T.b] 3.073 2.876 3.271 0.101 1998 30.477 0.0 ***

Bayesian

We can compute the equivalent dummy-coded regression model to estimate with bambi and the pymc3 backend

[8]:

b_model = bmb.Model(df)
res_b = b_model.fit('Val ~ Group', samples=1000, tune=1000)

Auto-assigning NUTS sampler...
INFO:pymc3:Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
INFO:pymc3:Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
INFO:pymc3:Multiprocess sampling (2 chains in 2 jobs)
NUTS: [Val_sd, Group, Intercept]
INFO:pymc3:NUTS: [Val_sd, Group, Intercept]
100.00% [4000/4000 00:03<00:00 Sampling 2 chains, 0 divergences] 
[9]:

# Model priors
b_model.plot();
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_14_0.png 
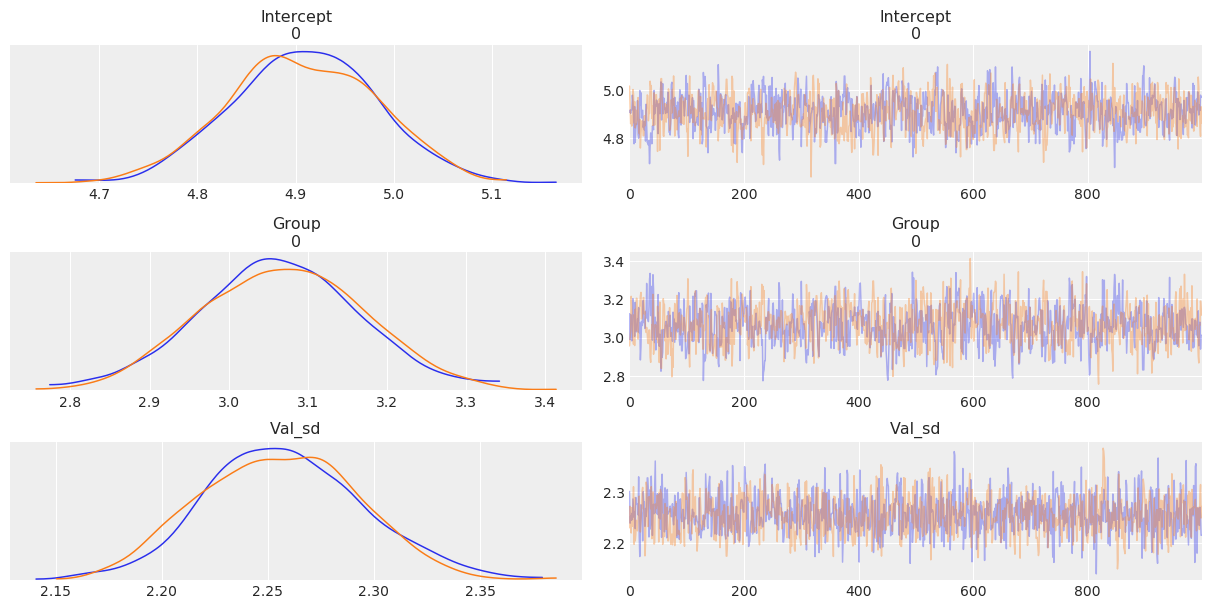
[10]:

az.plot_trace(res_b);
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_15_0.png 
[11]:

az.summary(res_b)

[11]:
mean sd hpd_3% hpd_97% mcse_mean mcse_sd ess_mean ess_sd ess_bulk ess_tail r_hat
Intercept[0] 4.908 0.073 4.775 5.047 0.003 0.002 780.0 780.0 788.0 1197.0 1.0
Group[0] 3.066 0.101 2.866 3.245 0.004 0.003 723.0 717.0 726.0 1067.0 1.0
Val_sd 2.257 0.037 2.193 2.329 0.001 0.001 1549.0 1545.0 1563.0 1408.0 1.0 
[12]:

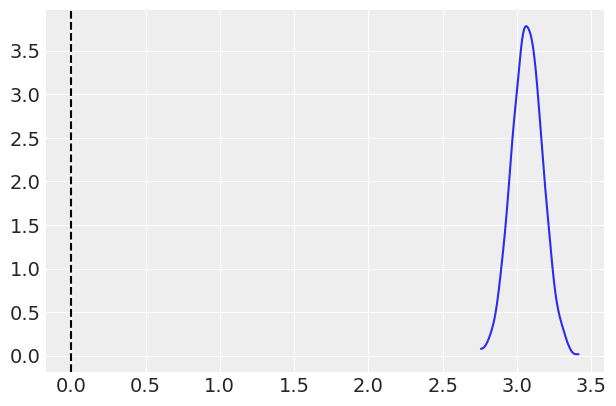
# Grab just the posterior of the term of interest (group)
group_posterior = res_b.posterior['Group'].values
ax = az.plot_kde(group_posterior)
ax.axvline(0, 0, 3, linestyle='--', color='k');
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_17_0.png 
[13]:

#Probabiliy that posterior is > 0
(group_posterior > 0).mean()

[13]:

1.0

Generate multi-level regression data

Generate data for a multivariate regression model with random intercepts and slope effect for each group

[14]:

# Simulate some multi-level data with pymer4
df, blups, coefs = simulate_lmm(num_obs=500, num_coef=2, num_grps=25, coef_vals=[5,3,-1])
df.head()
blups.head()

[14]:
Intercept IV1 IV2
Grp1 5.078462 2.965038 -0.809101
Grp2 5.038959 3.389151 -0.728827
Grp3 4.711509 2.892428 -1.009656
Grp4 4.916194 2.633570 -0.881529
Grp5 5.069100 3.195954 -1.023484

Frequentist multi-level model

[15]:

# Fit multi-level model using pymer4 (lmer in R)
model = Lmer('DV ~ IV1 + IV2 + (IV1 + IV2|Group)',data=df)
model.fit()

Model failed to converge with max|grad| = 0.0024797 (tol = 0.002, component 1)

Formula: DV~IV1+IV2+(IV1+IV2|Group)

Family: gaussian         Inference: parametric

Number of observations: 12500    Groups: {'Group': 25.0}

Log-likelihood: -17857.782       AIC: 35715.565

Random effects:

                 Name    Var    Std
Group     (Intercept)  0.057  0.238
Group             IV1  0.081  0.285
Group             IV2  0.055  0.235
Residual               0.998  0.999

               IV1  IV2   Corr
Group  (Intercept)  IV1 -0.020
Group  (Intercept)  IV2  0.149
Group          IV1  IV2 -0.115

Fixed effects:


[15]:
Estimate 2.5_ci 97.5_ci SE DF T-stat P-val Sig
(Intercept) 5.008 4.913 5.103 0.048 24.002 103.450 0.0 ***
IV1 3.015 2.902 3.128 0.058 24.031 52.268 0.0 ***
IV2 -0.897 -0.991 -0.803 0.048 24.000 -18.706 0.0 *** 
[16]:

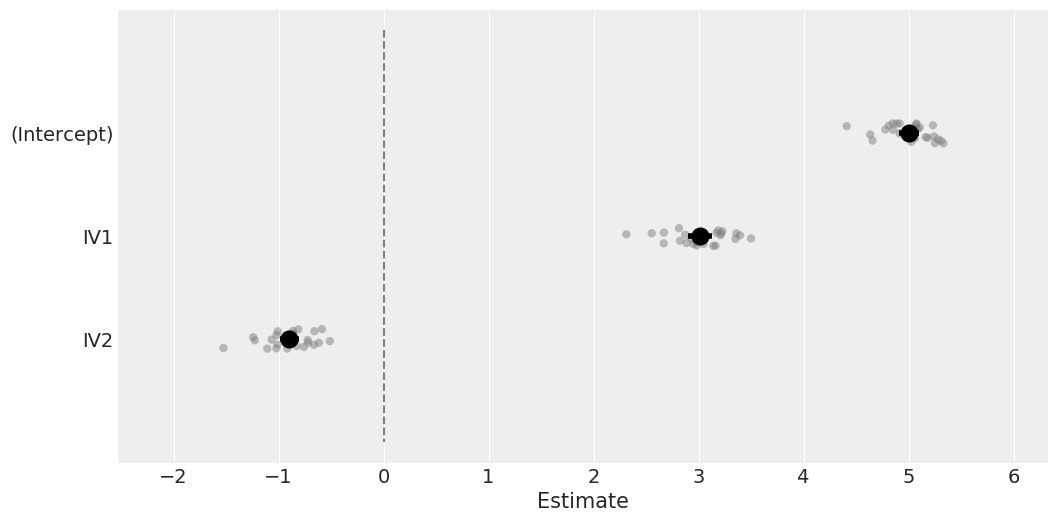
# Plot coefficients and the group BLUPs as well
model.plot_summary();
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_24_0.png 
[17]:

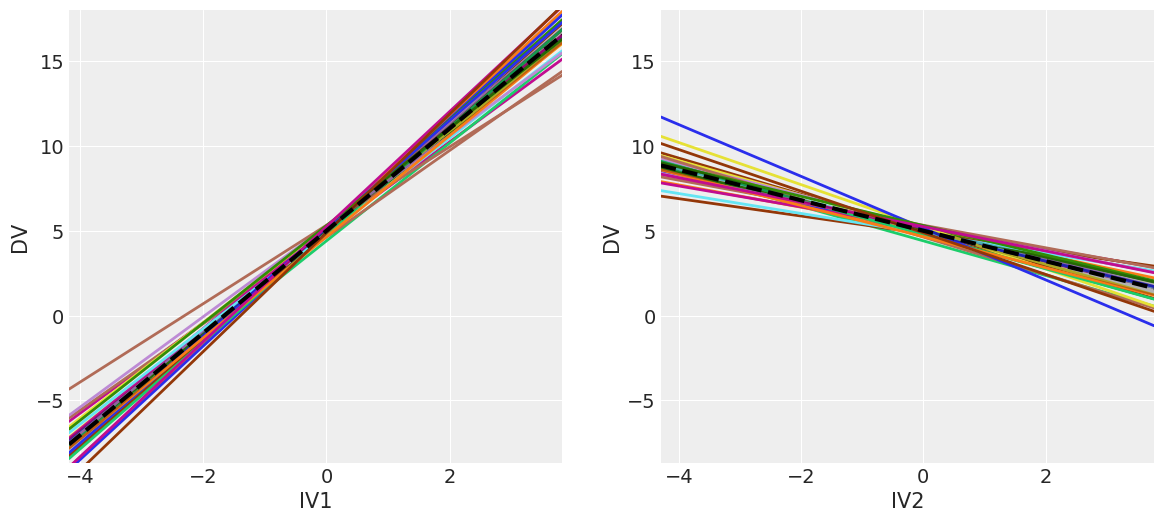
# Alternatively visualize coefficients as regression lines with BLUPs overlaid
_, axs = plt.subplots(1, 2, figsize=(14, 6))
model.plot('IV1', ax=axs[0],)
model.plot('IV2', ax=axs[1]);
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_25_0.png

Bayesian multi-level model

[18]:

b_model = bmb.Model(df)
results = b_model.fit('DV ~ IV1 + IV2',random=['IV1+IV2|Group'], samples=1000, tune=1000)

Auto-assigning NUTS sampler...
INFO:pymc3:Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
INFO:pymc3:Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
INFO:pymc3:Multiprocess sampling (2 chains in 2 jobs)
NUTS: [DV_sd, IV2|Group_offset, IV2|Group_sd, IV1|Group_offset, IV1|Group_sd, 1|Group_offset, 1|Group_sd, IV2, IV1, Intercept]
INFO:pymc3:NUTS: [DV_sd, IV2|Group_offset, IV2|Group_sd, IV1|Group_offset, IV1|Group_sd, 1|Group_offset, 1|Group_sd, IV2, IV1, Intercept]
100.00% [4000/4000 01:36<00:00 Sampling 2 chains, 0 divergences] 
The estimated number of effective samples is smaller than 200 for some parameters.
ERROR:pymc3:The estimated number of effective samples is smaller than 200 for some parameters.

[19]:

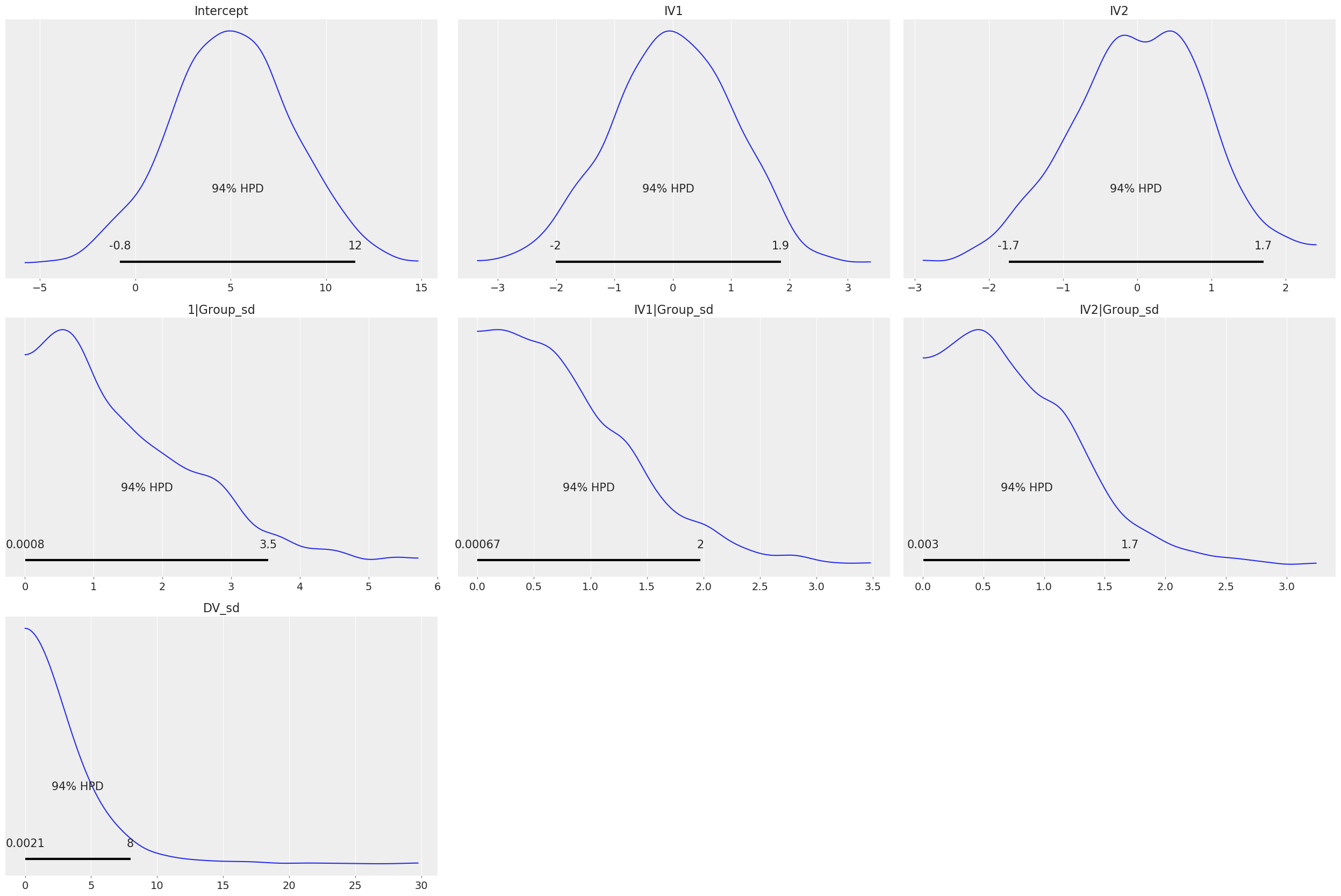
# Plot priors
b_model.plot();
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_28_0.png 
[20]:

#Plot posteriors
az.plot_trace(results, compact=True);
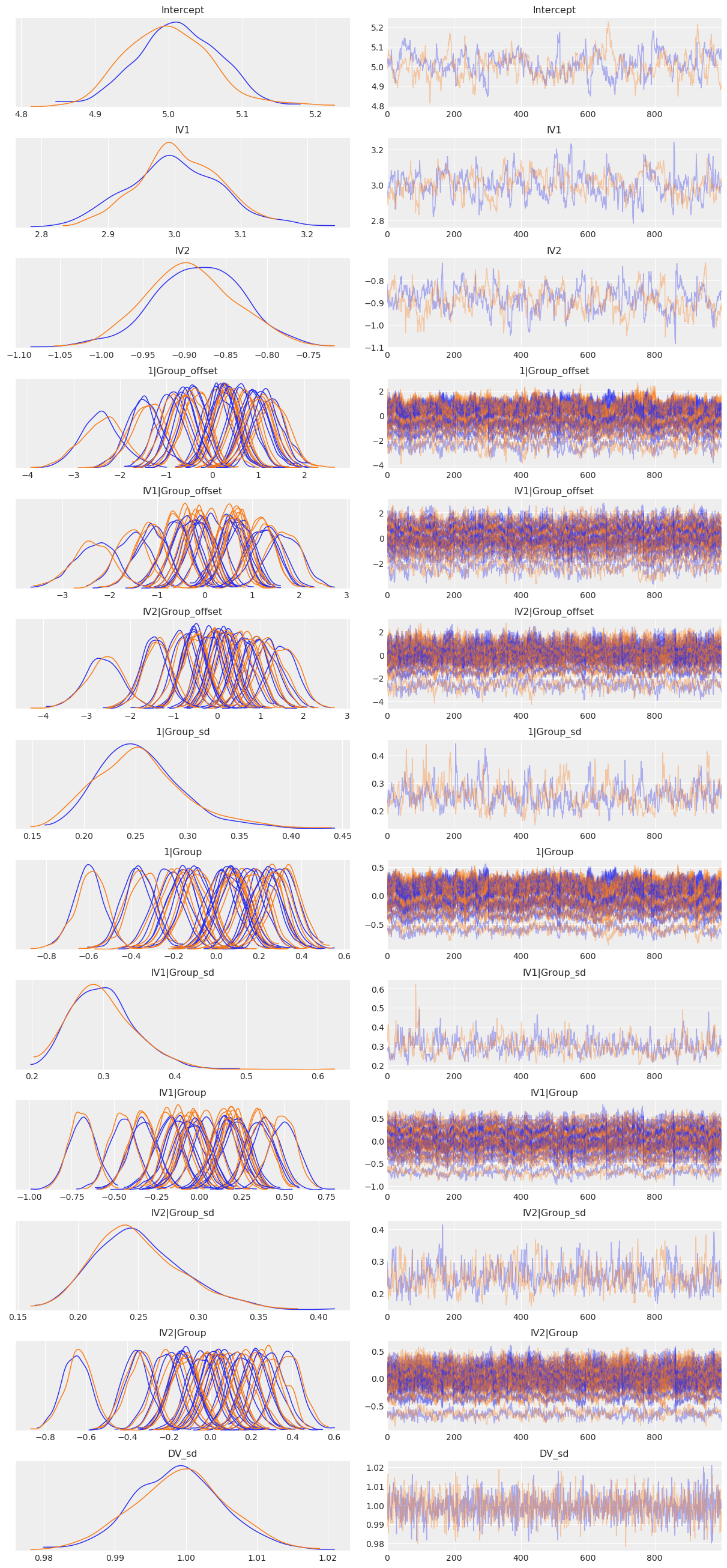
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_29_0.png 
[21]:

az.summary(results,
          var_names=['Intercept', 'IV1', 'IV2', '1|Group_sd', 'IV1|Group_sd', 'IV2|Group_sd', 'DV_sd'])

[21]:
mean sd hpd_3% hpd_97% mcse_mean mcse_sd ess_mean ess_sd ess_bulk ess_tail r_hat
Intercept[0] 5.007 0.059 4.903 5.117 0.005 0.003 142.0 141.0 143.0 256.0 1.01
IV1[0] 3.003 0.067 2.885 3.137 0.005 0.004 160.0 160.0 159.0 397.0 1.01
IV2[0] -0.888 0.055 -0.988 -0.779 0.005 0.003 146.0 144.0 146.0 298.0 1.01
1|Group_sd 0.255 0.043 0.175 0.334 0.003 0.002 221.0 221.0 216.0 457.0 1.00
IV1|Group_sd 0.300 0.045 0.218 0.382 0.003 0.002 314.0 314.0 309.0 622.0 1.01
IV2|Group_sd 0.251 0.038 0.183 0.322 0.002 0.001 322.0 322.0 319.0 559.0 1.00
DV_sd 0.999 0.007 0.988 1.012 0.000 0.000 1919.0 1919.0 1917.0 1526.0 1.00 
[22]:

az.plot_kde(results.posterior['IV1'], plot_kwargs={'color': 'C0'}, label='IV1')
az.plot_kde(results.posterior['IV2'], plot_kwargs={'color': 'C1'}, label='IV2')
az.plot_kde(results.posterior['Intercept'], plot_kwargs={'color': 'C2'}, label='Intercept')
plt.axvline(0, color='k', linestyle='--')
plt.legend();
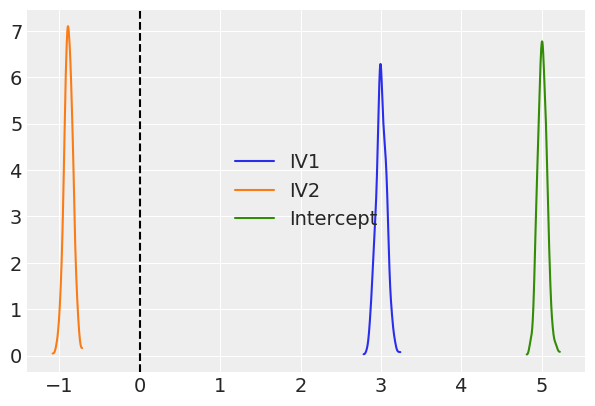
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_31_0.png

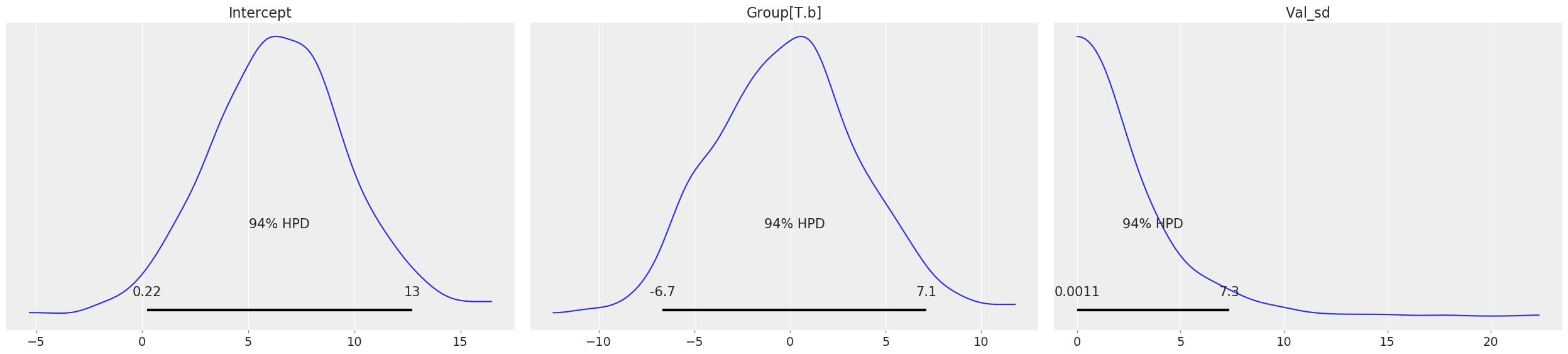
Because we used pymc3 for the backend estimation in bambi, we have access to few extra goodies. Here we make a forest plot similar to the one above for the frequentist model, but with 94% credible intervals instead

[23]:

# Credible interval plot using pymc3
# Line is 94% credible interval calculated as higher posterior density
# Inter quartile range is thicker line
# Dot is median
az.plot_forest(results, var_names=['Intercept', 'IV1', 'IV2', '1|Group_sd'], figsize=(10, 2));

INFO:numba.transforms:finding looplift candidates
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_33_1.png

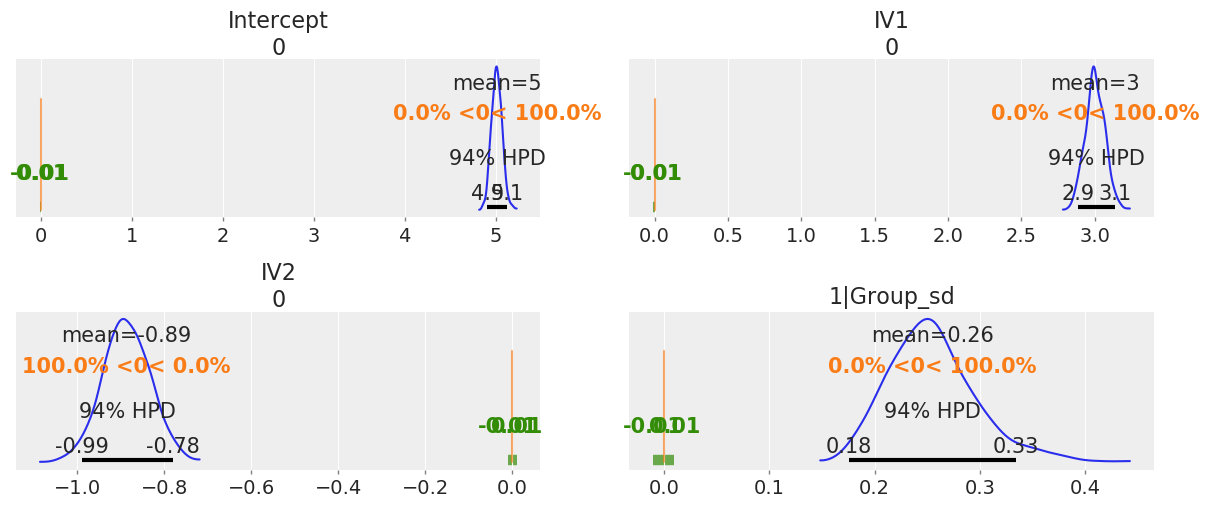
We can also plot the posterior overlayed with a region of practical equivalence (ROPE), i.e. range of values that were the coefficients to fall into, we might interpret them differently. We can see that all our posterior distributions fall outside of this range.

[24]:

# Show credible interval cutoffs, and also overlay region of practical equivalence (arbitrary, in this case close enough to 0 to not matter)
_, ax = plt.subplots(2, 2, figsize=(12, 5), constrained_layout=True)
az.plot_posterior(b_model.backend.trace,
                  var_names=['Intercept', 'IV1', 'IV2', '1|Group_sd'],
                  ref_val=0,
                  rope=[-.01, .01],
                  ax=ax);
../_images/notebooks_Bayesian_Frequentist_Tutorial_pymer4_35_0.png
Bayesian Logistic Regression Example Bayesian Multiple Regression Example